Sets and Relations¶

Sets¶

A set is a collection of unique, unordered elements. All Alloy expressions use sets of atoms and Relations. All elements of a set must all be either atoms, relations, or multirelations of the same arity, but may be different types of each category.

In expressions, the name of the signature is equal to the set of all atoms in that signature. The same is true for signature fields. Given

sig Teacher {}
sig Student {
  teacher: Teacher
}

Then the spec recognizes Student as the set of all atoms of type Student, and likewise with the Teacher signature and the teacher relationship.

Everything in Alloy is a set. If S1 is a Student atom, then S1 is the set containing just S1 as an element.

There are also two special sets:

none is just the empty set. Saying no Set is the same as saying Set = none. See Expressions.
univ is the set of all atoms in the model. In this example, univ = Student + Teacher.

Note

By default, the analyzer also generates a set of integers for each model, which will appear in univ. This can almost always be ignored in specifications (but see # below).

Set Operators¶

Set operators can be used to construct new sets from existing ones, for use in expressions and predicates.

S1 + S2 is the set of all elements in either S1 or S2 (set union).
S1 - S2 is the set of all elements in S1 but not S2 (set difference).
S1 & S2 is the set of all elements in both S1 and S2 (set intersection).

S1 = {A, B}
S2 = {B, C}

S1 + S2 = {A, B, C}
S1 - S2 = {A}
S1 & S2 = {B}

`->` used as an operator¶

Given two sets, Set1 -> Set2 is the Cartesian product of the two: the set of all relations that map any element of Set1 to any element of Set2.

Set1 = {A, B}
Set2 = {X, Y, Z}

Set1 -> Set2 = {
  A -> X, A -> Y, A -> Z,
  B -> X, B -> Y, B -> Z
}

As with other operators, a standalone atom is the set containing that atom. So we can write A -> (X + Y) to get (A -> X + A -> Y).

Tip

univ -> univ is the set of all possible relations in your model.

Integers¶

Alloy has limited support for integers. To enforce bounded models, the numerical range is finite. By default, Alloy uses models with 4-bit signed integers: all integers between -8 and 7. If an arithmetic operation would cause this to overflow, then the predicate is automatically declared false. In the Evaluator, however, it will wrap the overflowed number.

Tip

The numerical range can be changed by placing a scope on Int. The number of the scope is the number of bits in the signed integers. For example, if the scope is 5 Int, the model will have all integers between -16 and 15.

All arithmetic operators are over the given model’s numeric range. To avoid conflict with set and relation operators, the arithmetic operators are written as Functions:

add[1, 2]
sub[1, 2]
mul[1, 2]
div[3, 2] -- integer division, drop remainder
rem[1, 2] -- remainder

You can use receiver syntax for this, and write add[1, 2] as 1.add[2]. There are also the following comparison predicates:

=< 2
< 2
> 2
>= 2
!= 2
= 2

As there are no corresponding symbols for elements to overload, these operators are written as infixes.

Warning

Sets of integers have non-intuitive properties and should be used with care.

`#`¶

#S is the number of elements in S.

Sets of numbers¶

For set operations, a set of numbers are treated as a set. For arithmetic operations, however, a set of numbers is first summed before applying the operator. This is equivalent to using the sum[] function.

(1 + 2) >= 3 -- true
(1 + 2) <= 3 -- true
(1 + 2) = 3  -- false
(1 + 2).plus[0] = 3 -- true
(1 + 1).plus[0] = 2 -- false

Relations¶

Given the following spec

sig Group {}
sig User {
  belongs_to: set Group
}

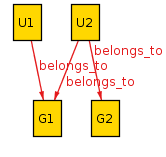
belongs_to describes a relation between User and Group. Each individual relation consists of a pair of atoms, the first being User, the second being Group. We write an individual relation with ->. One possible model might have

belongs_to = {
  U1 -> G1 +
  U2 -> G1 +
  U2 -> G2
}

Relations do not need to be 1-1: here two users map to G1 and one user maps to both G1 and G2.

Relations in Alloy are first class objects, and can be manipulated and used in expressions. [This assumes you already know the set operations]. For example, we can reverse a relation by adding ~ before it:

~belongs_to = {
  G1 -> U1 +
  G1 -> U2 +
  G2 -> U2
}

The . Operator¶

The dot (.) operator is the most common relationship operator, and has several different uses. The dot operator is left-binding: a.b.c is parsed as (a.b).c, not a.(b.c).

`Set.rel`¶

If Set is an individual atom, this returns all elements that said atom maps to. If Set is more than one atom, this gets all elements they map to.

U1.belongs_to = G1
(U1 + U2).belongs_to = {G1, G2}

Tip

In this case, we can find all groups in the relation with User.belongs_to. However, some relations may mix different types of atoms. In that case univ.~rel is the domain of rel and univ.rel is the range of rel.

For Multirelations, this will return the “tail” of the relation. Eg if rel = A -> B -> C, then A.rel = B -> C.

`rel.Set`¶

Writing rel.Set is equivalent to writing Set.~rel. See ~rel.

belongs_to.G1 = {U1, U2}
G1.~belongs_to = {U1, U2}

`rel1.rel2`¶

We can use the dot operator with two relations. It returns the inner product of the two relations. For example, given

rel1 = {A -> B,         B -> A}
rel2 = {B -> C,
        B -> D,         A -> E}

rel1.rel2 = {
        A -> C,
        A -> D,         B -> E}

In our case with Users and Groups, belongs_to.~belongs_to maps every User to every other user that shares a group.

Note

The operator isn’t overloaded; it’s the same operator with the same semantics for both Set.rel and rel1.rel2.

[]¶

rel[elem] is equivalent to writing elem.(rel). It has a lower precedence than the . operator, which makes it useful for Multirelations. If we have

sig Light {
   state: Color -> Time
}

Then L.state[C] would be all of the times T where the light L was color C. The equivalent without [] would be C.(L.state).

iden¶

iden is the relationship mapping every element to itself. If we have an element a in our model, then (a -> a) in iden.

An example of iden’s usefulness: if we want to say that rel doesn’t have any cycles, we can say no iden & ^rel.

Additional Operators¶

Note

You cannot use ~, ^, or * with higher-arity relations.

`~rel`¶

As mentioned, ~rel is the reverse of rel.

`^` and `*`¶

These are the transitive closure relationships. Take the following example:

sig Node {
  edge: set Node
}

N.edge is the set of all nodes that N connects to. N.edge.edge is the set of all nodes that an edge of N connects to. N.edge.edge.edge is the set of all nodes that are an edge of an edge of N, ad infinitum. If we want every node that is connected to N, this is called the transitive closure and is written as N.^edge.

^ does not include the original atom unless it’s transitively reachable! In the above example, N in N.^edge iff the graph has a cycle containing N. If we want to also include N, use N.*edge instead.

^ operates on the relationship, so ^edge is also itself a relationship and can be manipulated like any other. We can write both ~^edge and ^~edge. It also works on arbitrary relationships. U1.^(belongs_to.~belongs_to) is the set of people that share a group with U1, or share a group with people who share a group with U1, ad infinitum.

Warning

By itself *edge will include iden! *edge = ^edge + iden. For best results only use * immediately before joining the closure with another set.

Advanced Operators¶

`<:` and `:>`¶

<: is domain restriction. Set <: rel is all of the elements in rel that start with an element in Set. :> is the range restriction, and works similarly: rel :> Set is all the elements of rel that end with an element in Set.

This is mostly useful for directly manipulating relations. For example, given a set S, we can map every element to itself by doing S <: iden. We can also use restrictions to disambiguate overloaded fields. If we have

abstract sig Node {
  , edges: set Node
}

some sig Red, Blue extends Node {}

Then Blue <: edges :> Red is the set of all edges from Blue nodes to Red ones.

`++`¶

rel1 ++ rel2 is the union of the two relations, with one exception: if any relations in rel1 that share a “key” with a relation in rel2 are dropped. Think of it like merging two dictionaries.

Formally speaking, we have

rel1 ++ rel2 = rel1 - (rel2.univ <: rel1) + rel2

Some examples of ++:

(A -> B + A -> C) ++ (A -> A) = (A -> A)
(A -> B + A -> C) ++ (A -> A + A -> C) = (A -> A + A -> C)
(A -> B + A -> C) ++ (C -> A) = (A -> B + A -> C + C -> A)
(A -> B + B -> C) ++ (A -> A) = (A -> A + B -> C)

It’s mostly useful for modeling Time.

Note

When using multirelations the two relations need the same arity, and it overrides based on only the first element in the relations.

Set Comprehensions¶

Set comprehensions are written as

{x: Set1 | expr[x]}

The expression evaluates to the set of all elements of Set1 where expr[x] is true. expr can be any expression and may be inline. Set comprehensions can be used anywhere a set or set expression is valid.

Set comprehensions can use multiple inputs.

{x: Set1, y: Set2, ... | expr[x,y]}

In this case this comprehension will return relations in Set1 -> Set2.

Sets and Relations¶

Sets¶

Set Operators¶

-> used as an operator¶

Integers¶

#¶

Sets of numbers¶

Relations¶

The . Operator¶

Set.rel¶

rel.Set¶

rel1.rel2¶

[]¶

iden¶

Additional Operators¶

~rel¶

^ and *¶

Advanced Operators¶

<: and :>¶

++¶

Set Comprehensions¶

`->` used as an operator¶

`#`¶

`Set.rel`¶

`rel.Set`¶

`rel1.rel2`¶

`~rel`¶

`^` and `*`¶

`<:` and `:>`¶

`++`¶